invspec
2D Discrete Inverse Spectral Problem
Goal
To calculate an approximate solution to the classic (Laplace-Beltrami) inverse spectral problem for discrete (genus 0) surfaces.
Content
Included is a suite of MATLAB codes implementing the naive direct gradient descent approach.
test_script.m is the top-level script that generates results.
People
Project envisioned, advised, and supervised by Prof. Etienne Vouga and Prof. Keenan Crane
Some codes here (on mesh optimization and a demo of spherical harmonics) are not mine.
Testing Procedures
-
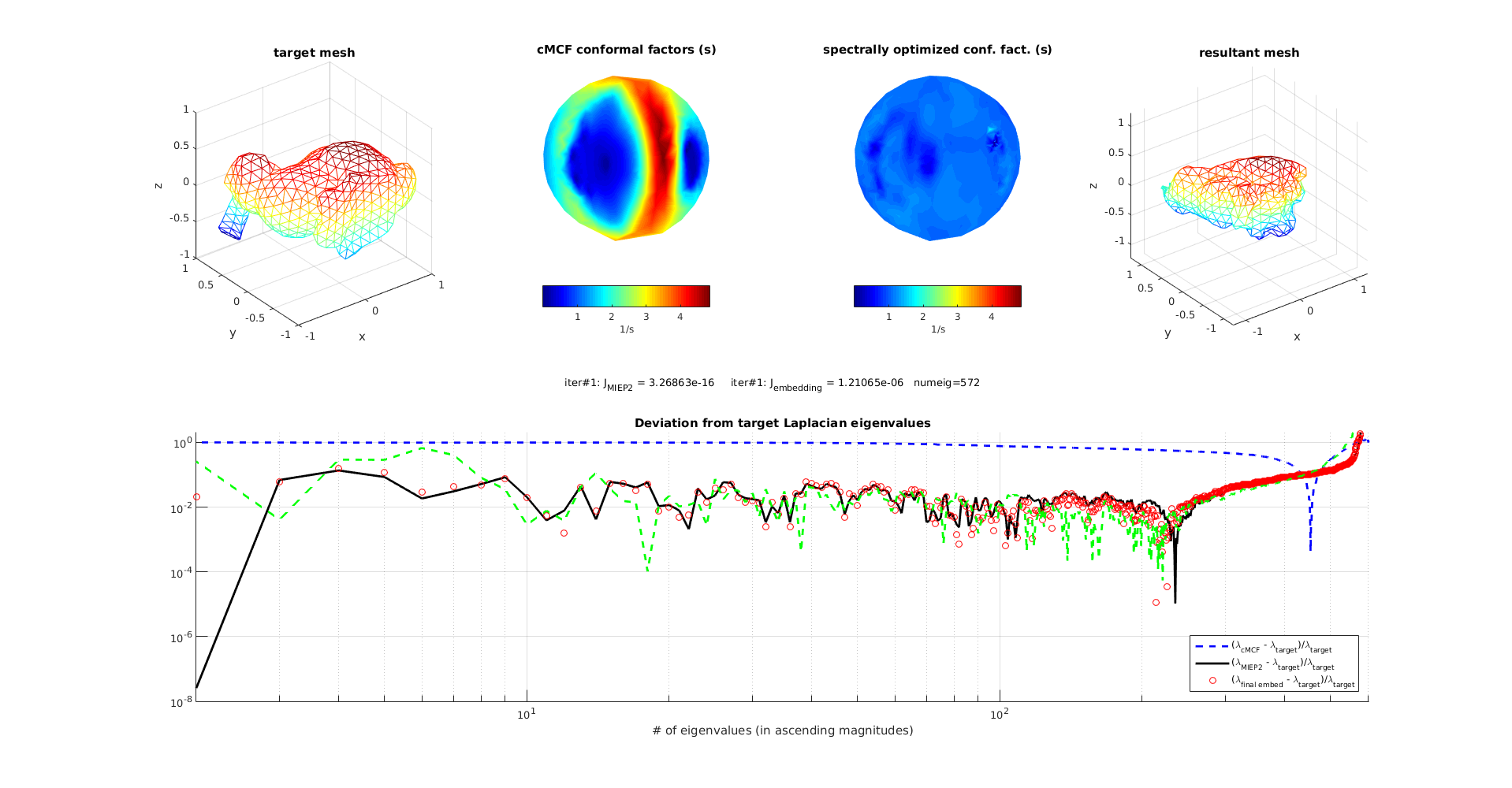
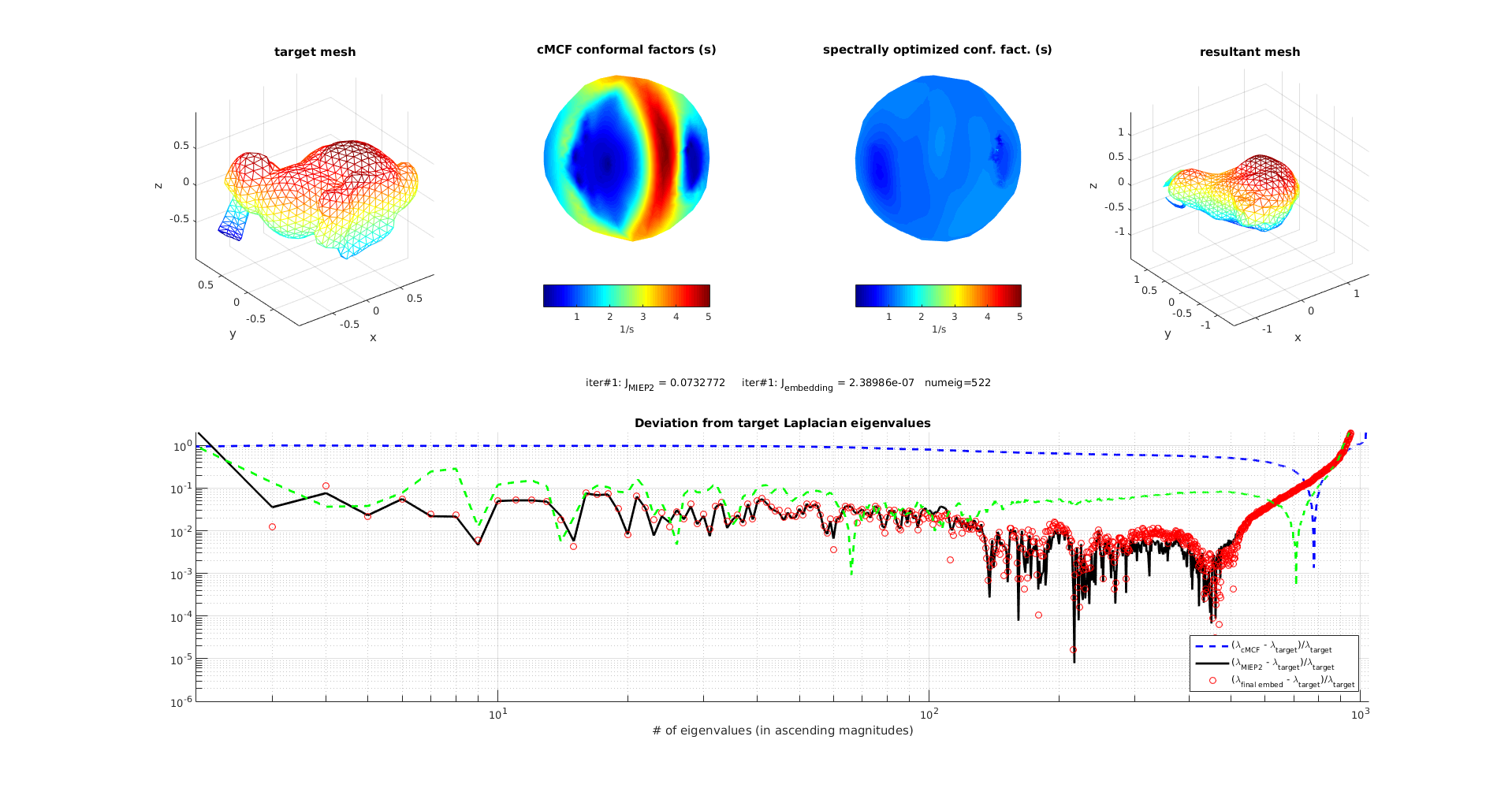
use conformalized mean curvature flow (cMCF) to get a spherical mesh with a target set of conformal factors from a target mesh
-
use BFGS descent search for some conformal factors that achieve a spectrum similar to the one desired
-
embed the metric to a resulting mesh from the sphere by optimizing edge lengths obtained from the factors
-
compare with the target mesh, target spectrum, and cMCF conformal factors
Results
)_e0.1-1p0.5.gif "discrete Y33 spherical harmonic target with varying percent of eigenvalues used")
)_e0.1p0.5-2.gif "discrete Y32 spherical harmonic target with varying amount of deformation")
(cheating) optimize for cMCF spectrum instead
)_e0.1p0.5-2.gif "discrete Y32 spherical harmonic target with varying amount of deformation")
Tests with Spot the cow
smoothed cow without bi-laplacian regularization
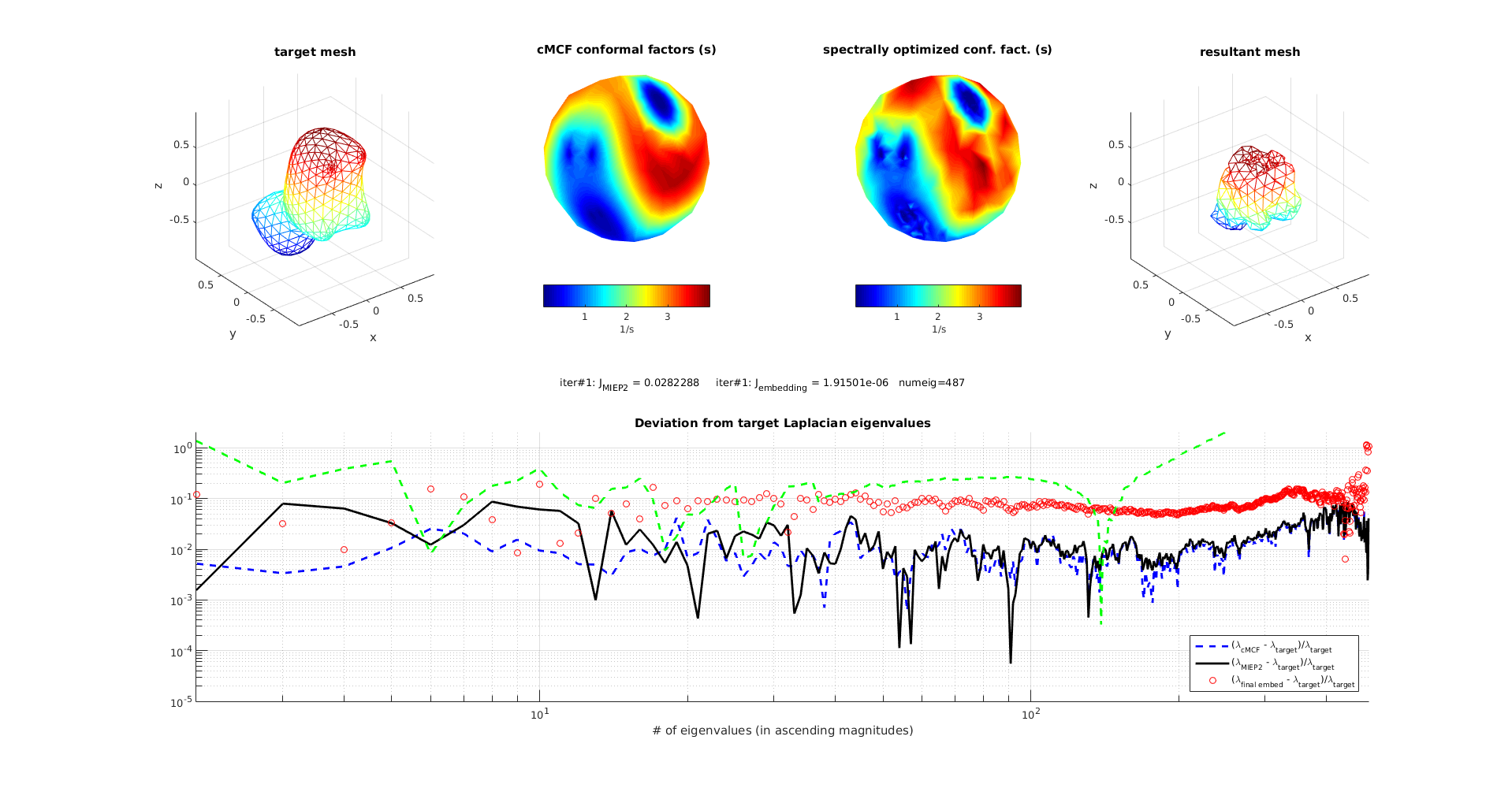
original spot with regularization
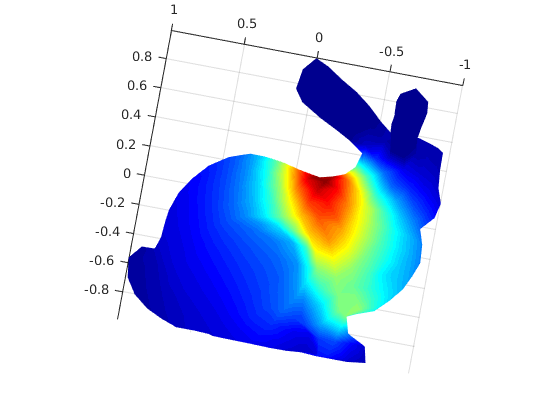
Tests with bunny
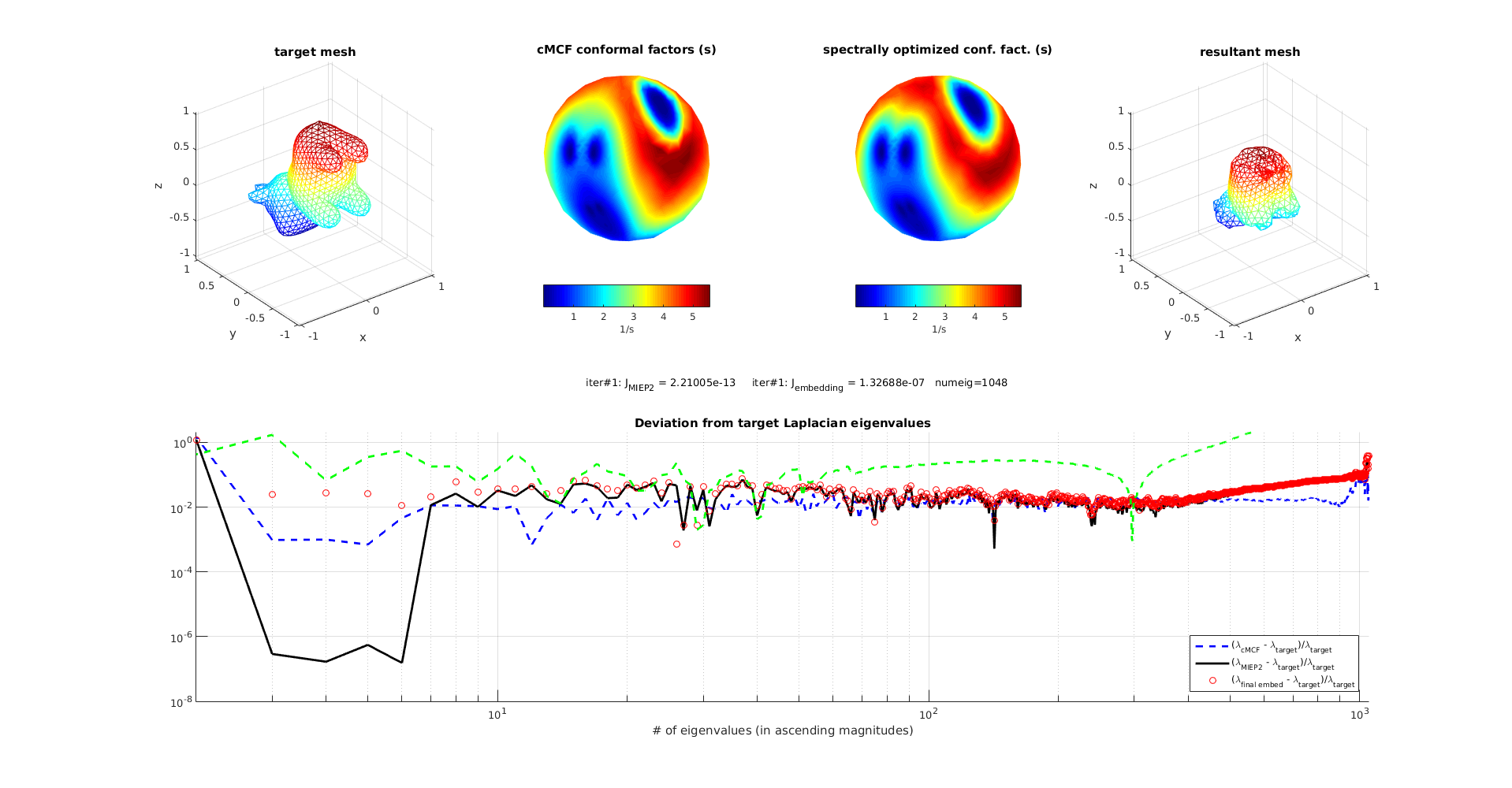
recursive run
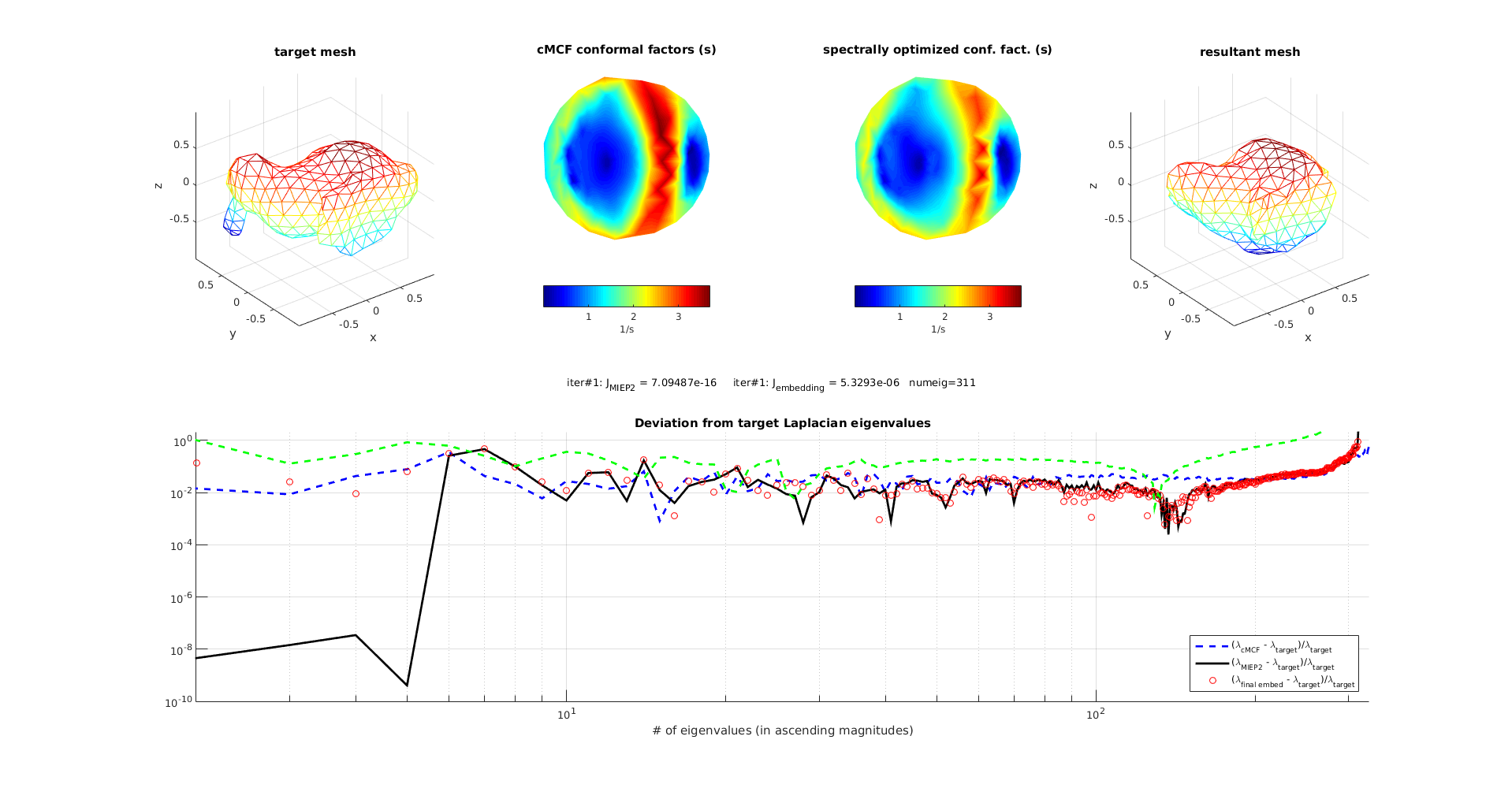
finer mesh recursive run
Before and After (with minor smoothing)
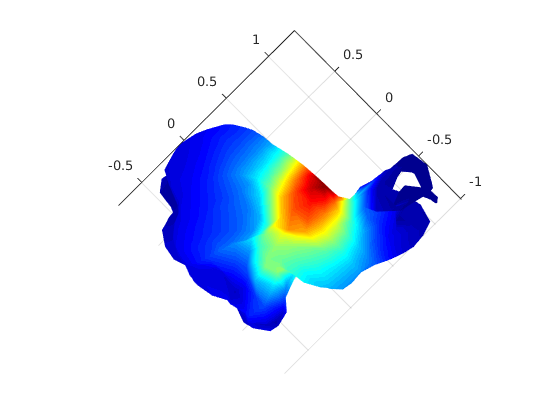
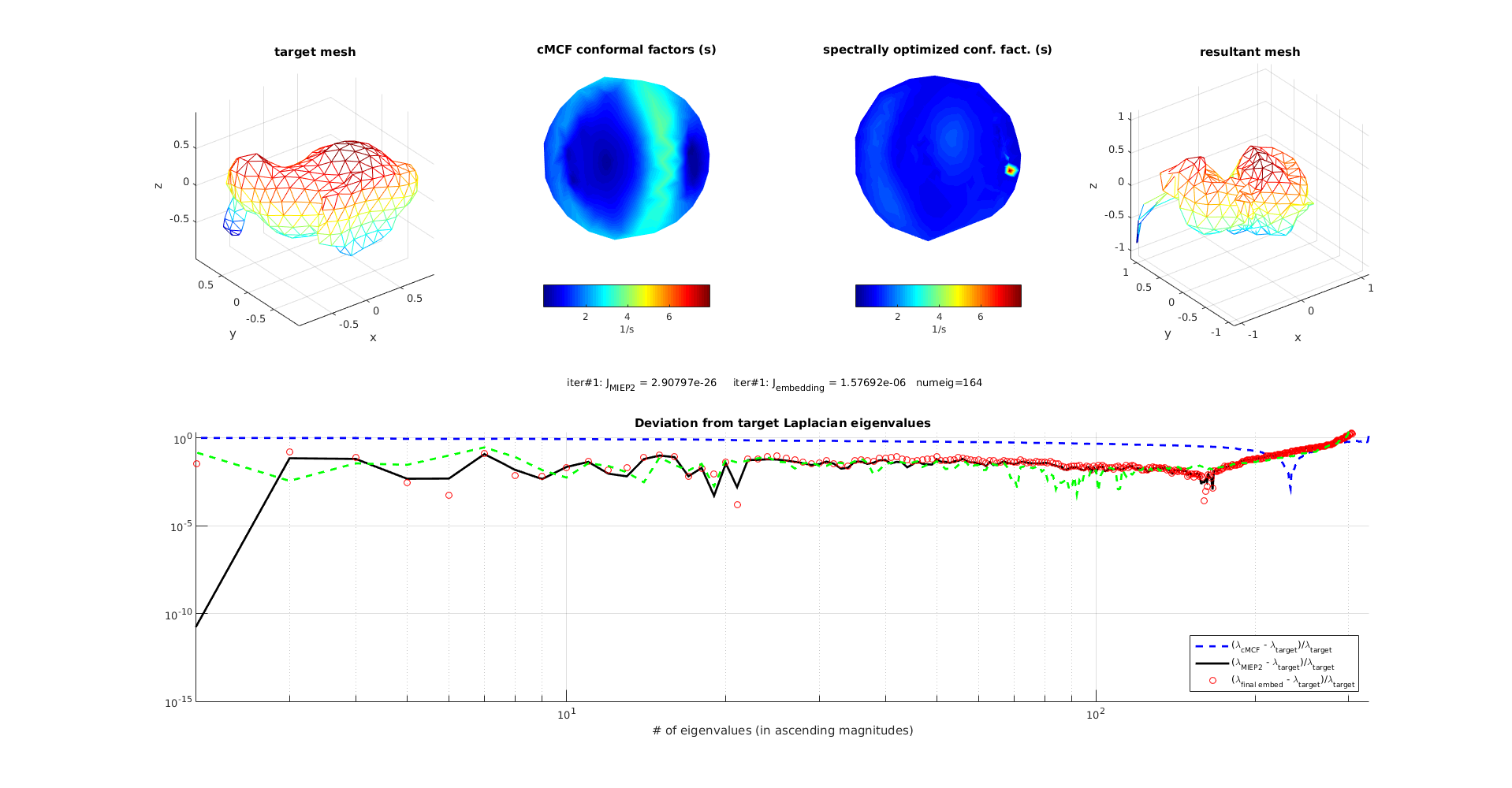
even finer mesh recursive run
“Mesh-free” Spherical Harmonic Basis Solution
From now on we have number of eigenvalues used = number of free SH basis function coefficient = n, LB operator expanded in 961 SH basis functions
PL spectrum as target: n = 36
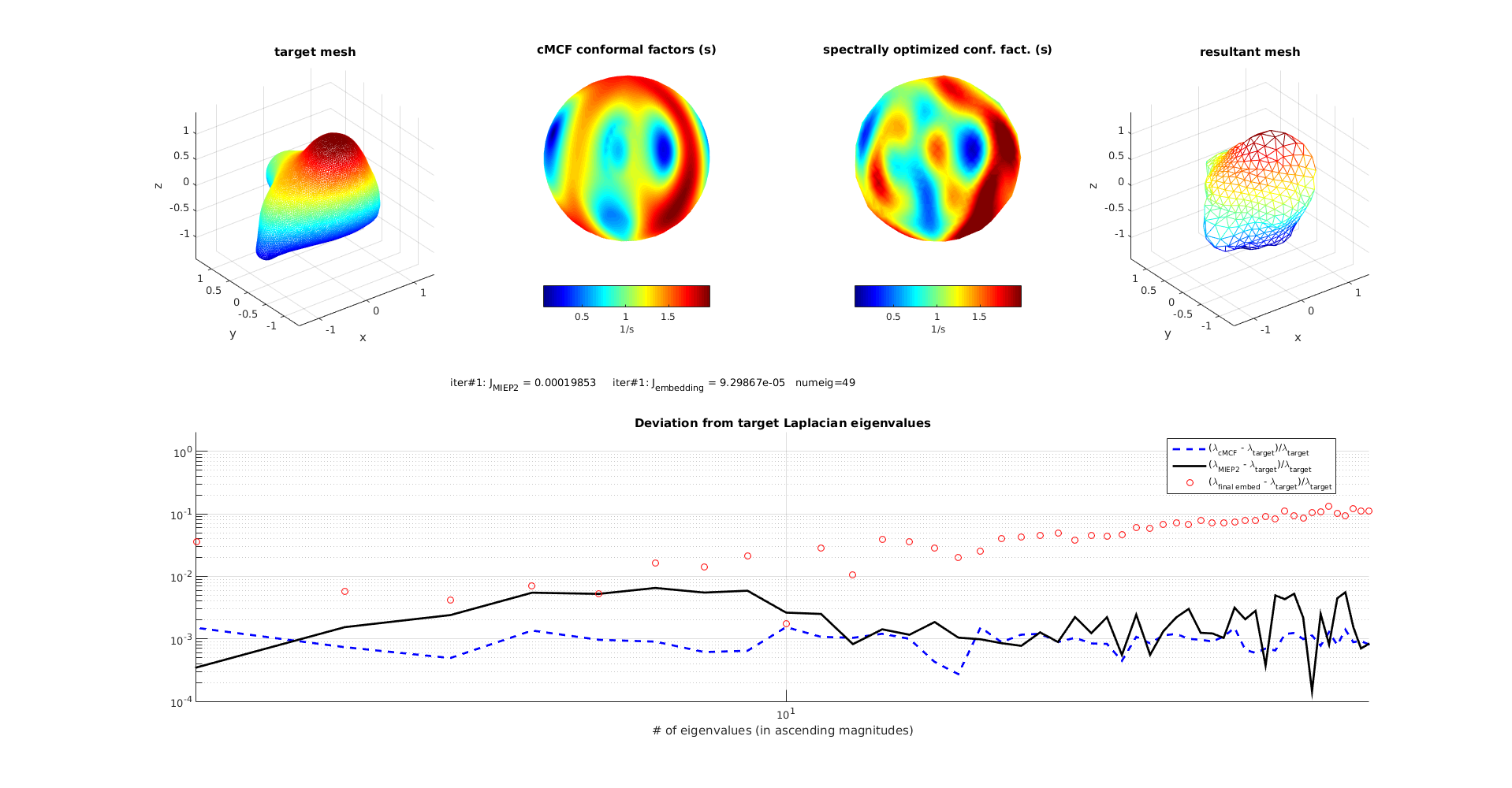
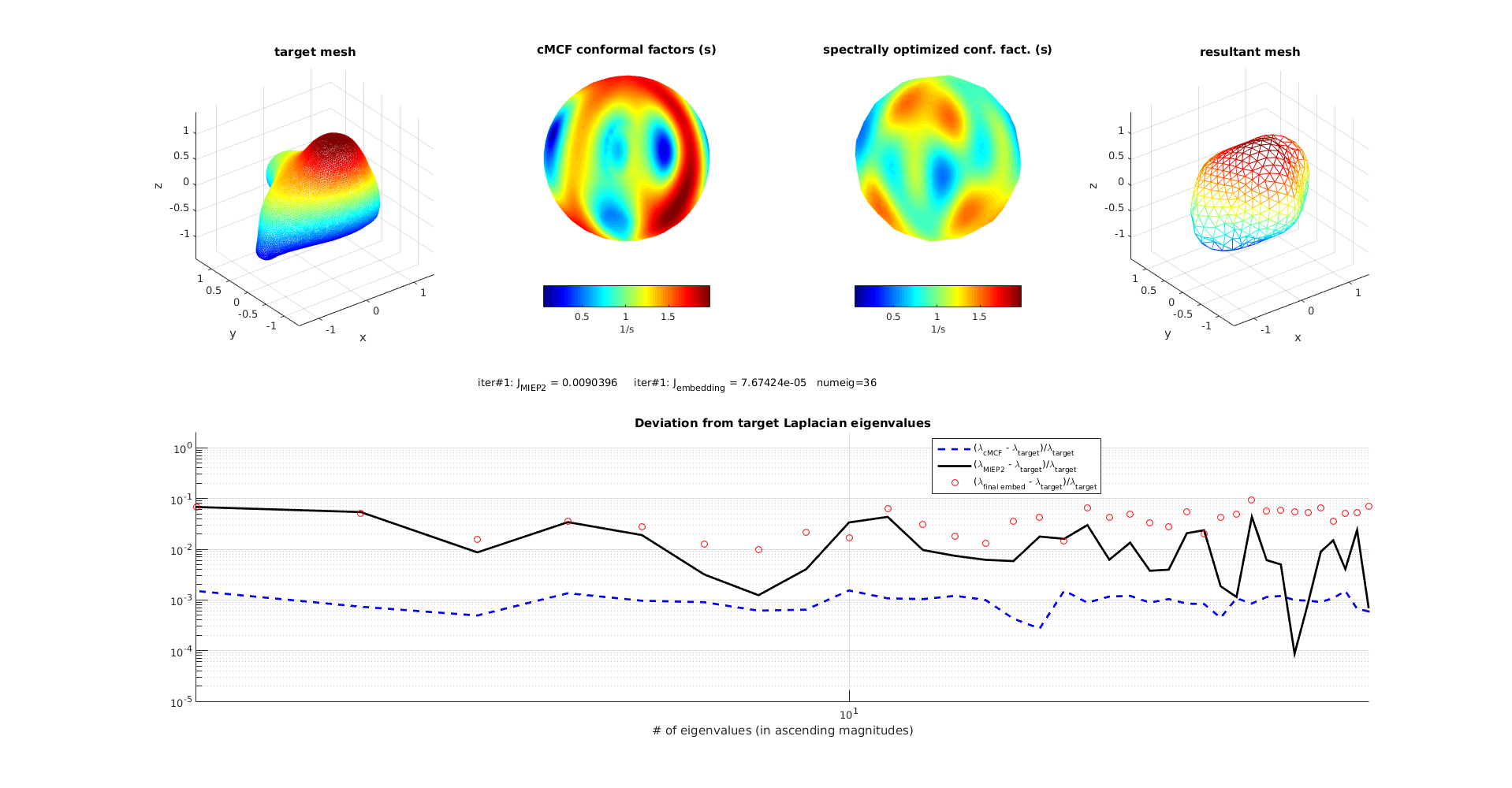n = 49
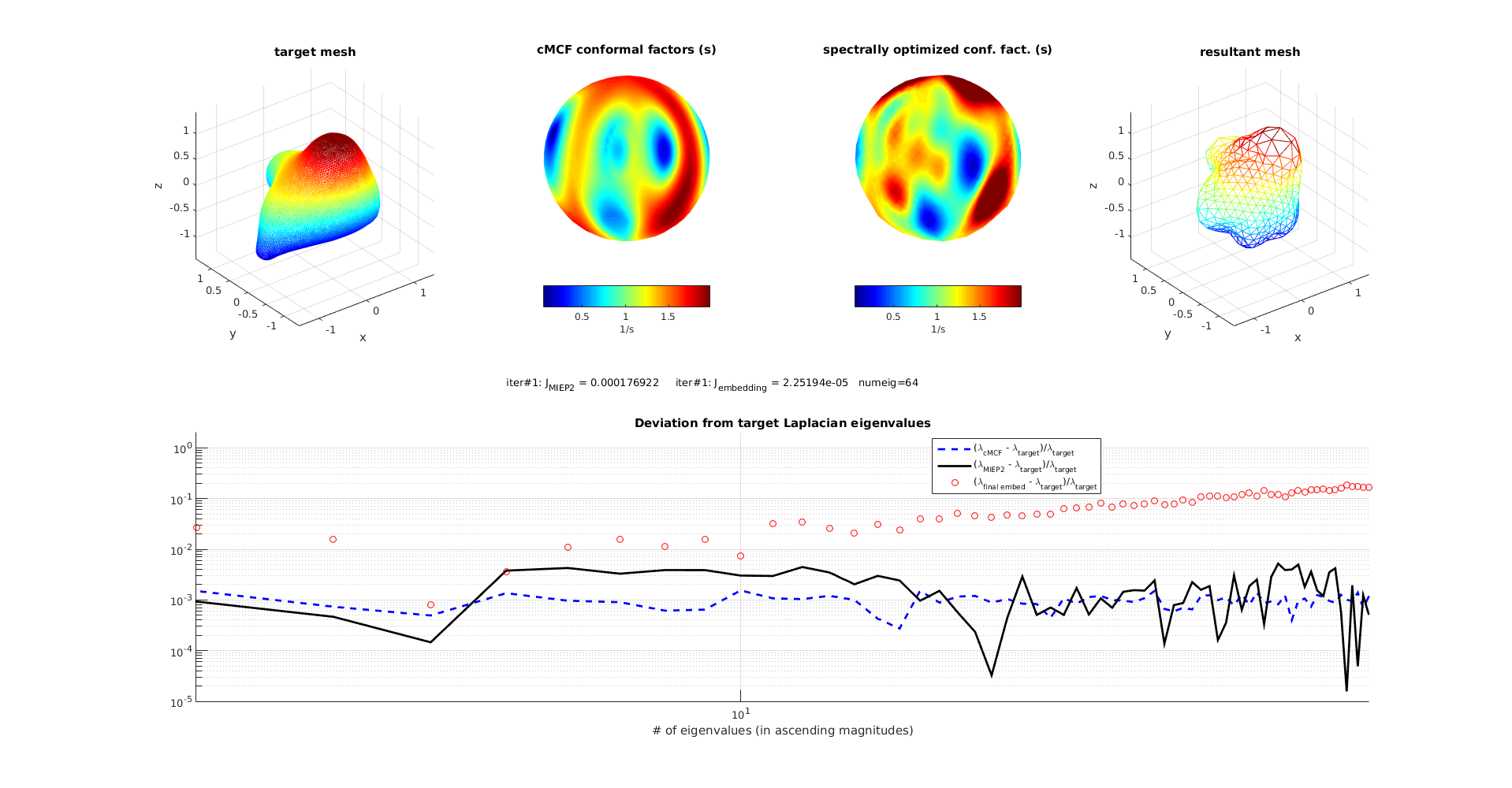
n = 64
SH spectrum as target (cheating): n = 49
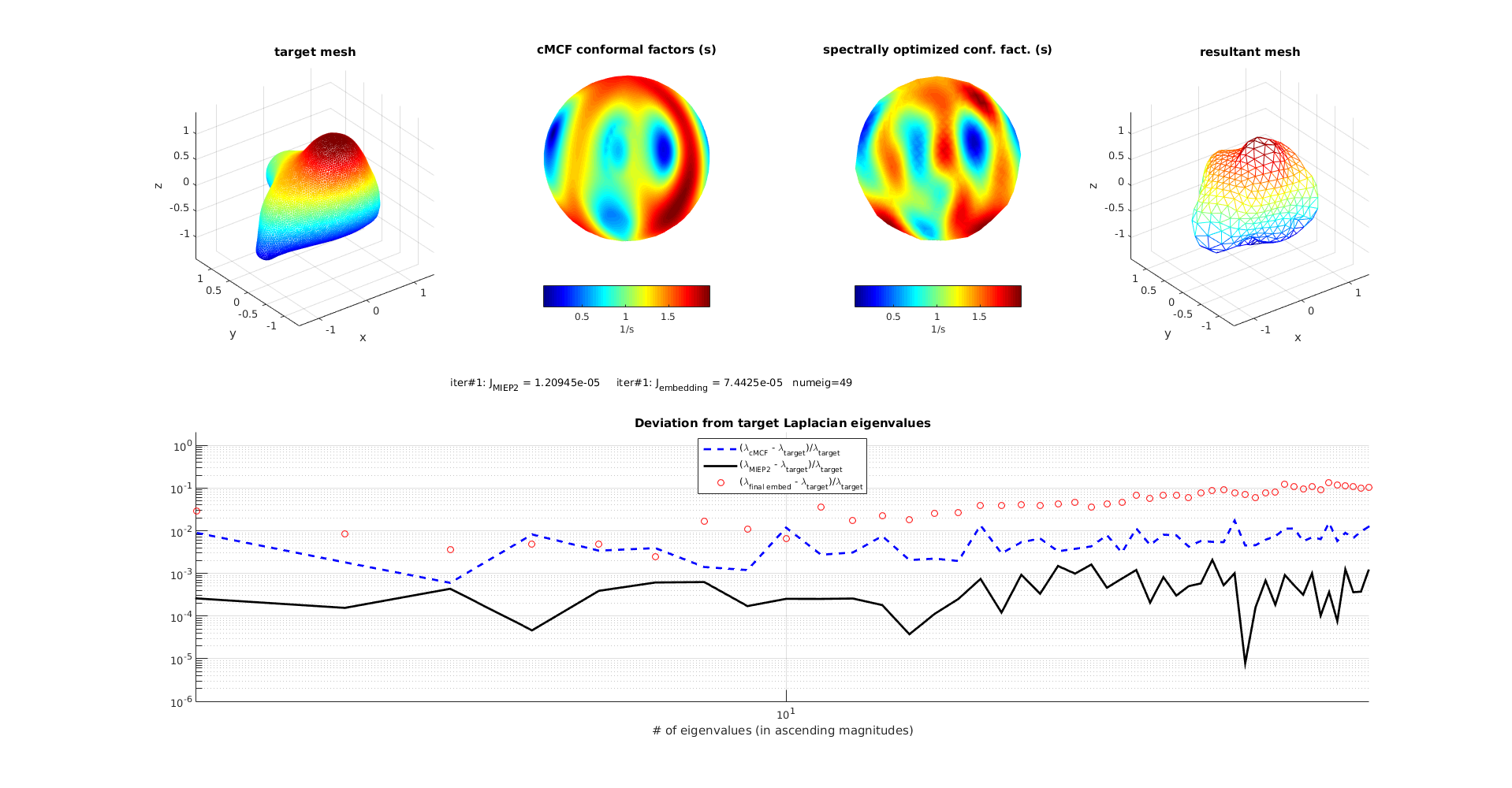
Results were adjusted up to SO(3) to mod out the rigid rotation ambiguity
Ways to go
-
(ongoing) without prior knowledge of the target mesh, we will have to start from a uniform (coarse) spherical mesh and develop a suitable adaptive refinement scheme
-
(banging my head) why does high frequency data matter in the FEM/hat function basis? the current way involves optimizing for them and then penalize for its noisyness via regularization, which seems very silly…
-
in practice the inverse problem would not be about the Laplace-Beltrami operator (need to consider bending energy of thin shell etc.)
-
in practice higher frequencies will most definitly be prohibitively noisy
-
can we guess the topology beforehand? would higher genus surfaces work in similar fashion despite planarity/hyperbolicity? (e.g. there are known non-trivial isospectral hyperbolic (g>5) surfaces…) (Yes. Reuter, Wolter, Peinecke 2006 ~ first 500 eigenvalues)